Study of Probability
Lesson 1: Probability models and axioms
| topic | details |
|---|---|
| What is probability? | a framework that dealing with uncertainty How to setup a probability model? basic rules of |
| Probability models Sample space Discrete Sample space |
Sample space, sets 1. list should be mutually exclusive 2. should be collectively exhaustive You can also use T+ H , raining, + H, not raining in coin flip, it's allowed Discrete Sample space, Dice experiment Use a sequential description or tree-based description 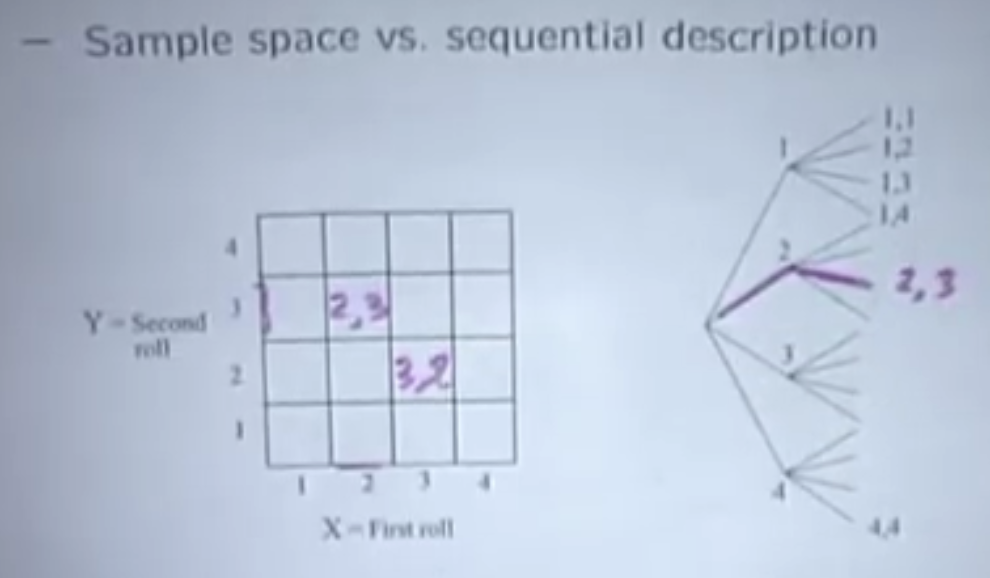 it's 2 stage. It's has a sample space which is finite. |
| Continuous Sample space | sample space is infinite. assign probabilities to individual outcome has zero probability, so we assign probabilities to subsets |
| Ground rules | 1. probabilities be number between 0 to 1 2. Probabilities should be Non-negativity: $$P(A)>=0$$ 3. total probabilities sum=1, $$P(\Omega)=1$$ 4. Additivity: if A and B have no common, then $$if A\cap B=\Theta , P(A \cup B) = P(A)+P(B)$$ union of 3 sets,$$ P(A\cup B\cup C) = P((A\cup B)\cup C)=P(A)+P(B)+P(C)$$ it can repeat to any N sets. if A1....Am, disjoint. |
| subtleties | 1. Additivity axiom doesn't quite do the job for everything we would like to do 2. has to do with weird sets, An event is a subset of the sample space, does this mean that we are going to assign probability to every possible subset of the sample space? -- we'd like to, but not always possible, but we are not going to encounter these sets |
| laws | Discrete uniform law: if all outcomes are equally likely(N of them ). then p(A)=1/N Continuous uniform law: Probability = Area P(X,Y)=0 , any point area =0 |
Lesson 2: Conditioning and Bayes' rule
All informations is always partial, what do we do to probabilities if we have some partial informations?
this lesson introduce 3 very useful ways, these ways break problem to simple pieces. infer things we have not seen.
| Topic | details | |
|---|---|---|
| Review | set up a model, first is come up with list of all possible outcomes. this is a sample space. 1. distinguishable from each other 2. mutually exclusive how to choose your sample space, depending on how much details you want to capture. its a art. assign subsets, disjoint subsets behave like masses, 0 probability things is not impossible, its only very very low possible. problem solving: - Specify sample space - Define probability law - Identify event of interest - Calculate |
|
| New information | you set up a model, and somebody give you a New Information, we should revise our beliefs. $$P(A\mid B) = Probability\ of\ A, given\ that\ B\ occurred$$ |
|
| How do we revise the probability that A occurs? |  Intuitively reasonable way: P(A|B)= part of the A in B.= 2(1+2) definition: $$P(A\mid B)=\frac{P(A\cap B)}{ P(B)}$$ so P A intersection B is the probability of B times the conditional probability $$P(A\cap B)= P(B)P(A\mid B) =P(A)P(B\mid A)$$ |